2020年/02月/16日
关于欧拉等式
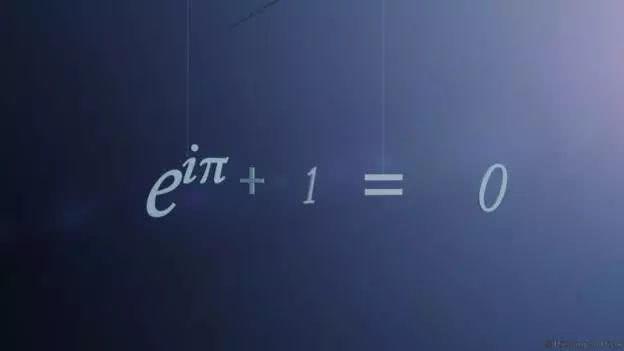
高斯曾说:“如果一个人第一次看到这个公式而不感受到它的魅力,那么他不可能成为数学家。”
理查德·费曼把她唤作“欧拉的宝石”
Euler’s identity is an equality found in mathematics that has been compared to a Shakespearean sonnet and described as “the most beautiful equation.” It is a special case of a foundational equation in complex arithmetic called Euler’s Formula, which the late great physicist Richard Feynman called in his lectures “our jewel” and “the most remarkable formula in mathematics.”
她端庄大方,秀外慧中,简洁包含着深刻。悬挂于巴黎发明宫数学陈列室的间墙,如莎士比亚的十四行诗,达·芬奇的蒙娜丽莎,王羲之的兰亭集序,人人都可驻足欣赏,顶礼膜拜。

玄兮妙兮,欧拉公式,她是数学美的金科玉律。
宫商角徵羽,声韵合于五音;金木水火土,万物化于五行;10πei,等式成于五数。五个最重要的常数,用加乘幂等系于一线,熔于一炉。
道生一,一生二,二生三,三生万物。自然数1,是整数的单位,是数字的始祖。
无为有处有还无。中性数0,空间原点,非正非负,亦庄亦谐,加之减之而不变,乘之则归尽,除之则无穷。
山巅一寺一壶酒,地老天荒无尽头。圆周率π,脍炙人口,妇孺皆诵。割圆祖率,幂级展开;无理数,超越数,正态数?计算证明,永无止境。
自然对数,顺其自然,以e为底,简洁方便。是欧拉首先将e作为专门的数学符号使用。人口增长、生存竞争、布朗运动、冷却定律……e无处不在,宛若美神,赋予各种函数和公式最洒脱的形式。
太虚幻境,即是真如福地。欧拉首先使用符号i=-1√,以更深的认识为数学王国又开辟出一块疆域,从此方程求根,交流电的表示……各种计算都面貌一新。
五朵金花,各放异彩,天造地设,珠联璧合。
名兮贵兮,欧拉公式,她是数学家的智慧结晶。
1、自然数的“e”含于其中。 自然对数的底,大到飞船的速度,小至蜗牛的螺线,谁能够离开它?
2、最重要的常数 π 含于其中。 世界上最完美的平面对称图形是圆。“最伟大的公式”能够离开圆周率吗? (还有π和e是两个最重要的无理数!)
3、最重要的运算符号 + 含于其中。 之所以说加号是最重要的符号,是因为其余符号都是由加号派生而来。减号是加法的逆逆运算,乘法是累计的加法……
4、最重要的关系符号 = 含于其中。 从你一开始学算术,最先遇见它,相信你也会同意这句话。
5、最重要的两个元在里面。零元0 ,单位1 ,是构造群,环,域的基本元素。如果你看了有关《近世代数》的书,你就会体会到它的重要性。
6、最重要的虚单位 i 也在其中。 虚单位 i 使数轴上的问题扩展到了平面,而在哈密尔的 4 元数与 凯莱的 8 元数中也离开不了它。 之所以说她美,是因为这个公式的精简。她没有多余的字符,却联系着几乎所有的数学知识。 有了加号,可以得到其余运算符号; 有了0,1,就可以得到其他的数字; 有了 π 就有了圆函数,也就是三角函数; 有了 i 就有了虚数,平面向量与其对应,也就有了哈密尔的 4 元数,现实的空间与其对应; 有了 e 就有了微积分,就有了和工业革命时期相适宜的数学。
The expression possesses Euler’s number ‘e’, the base of natural logarithms that is extensively recruited in calculus. It is a transcendental number whose value is 2.71828….
It possesses ‘i’, the complex or imaginary unit, which is the square root of -1 or the solution of the function ‘x²+1=0’. It is of utmost importance in electrical engineering and has provided great insights in quantum mechanics.
It possesses ‘π’, another transcendental number obtained by the ratio of a circle’s circumference to its diameter. Its value is 3.14159… This constant does not need any further introduction, as it is the most popular mathematical constant, ubiquitous in fields from Euclidian geometry to General Relativity.
It possesses the first natural number ‘1’, the multiplicative identity — any number multiplied by this identity results in the same number itself.
It possesses the first whole number ‘0’, the additive identity – any number added to this identity results in the same number itself.
这个欧拉公式的神奇之处在于,它把数学中最基本的五个常数,以非常优美的形式结合了起来:
e——自然对数,代表了大自然
π——圆周率,代表了无限
i——虚数单位,代表了想象
1——数字一,代表了起点
0——数字零,代表了终点
乘法代表结合,指数代表加成,加法代表累计,等号代表统一。
欧拉公式暗示着:大自然充满无限想象,但是最终都会归于终点。
欧拉恒等式让每个数学家看到了一个新的方向,一个伟大的蓝图,那就是大自然最基本的构造形式,并不是单独区分的,而是有着无可分割的联系,而这个联系并不是我们想象的那样复杂,而是像这个公式一样,无比的简洁,又无比的有力,像一首优雅的口风琴曲,悦耳悠扬。
无论什么样的语言都不能描述出欧拉恒等式的魅力,因为它本身就不是人类能言明的“神迹”它的存在表明了大自然拥有着人类远远无法想象的神奇和壮丽。
没有人能够想象当更多的“欧拉恒等式”呈现在我们面前的时候,会是什么样的情景,如果在人类以外真的还有文明,那么即便是他们看到了欧拉恒等式,也会感慨我们这个文明已经跨入了智慧的行列。
诗韵说:数学是如此的神奇不可思议,在外行人的眼中,这只是一行行无聊的符号和数字,但是在数学家眼中,它们就是这个宇宙最深奥的秘密,是大自然运转的法则,简简单单的几个字符就能揭示一个世界的真相,还有什么能够比数学更强大的“武器”呢?难怪有哲学家说,语言是人类的哲学,数学是上帝的哲学,当我们真正领悟这一点,或许就能真正感受到“欧拉恒等式”的魅力吧