18日
首页 回退

各种语言的的四则运算AST实现

写一个求值器，我们一般从四则运算表达式开始，我们从小到大写的代数表达式都是中缀表达式，它必须依赖括号来去除歧义，比如 12 * （24 - 5 ) / (17 + 6) ，其实还有另外两种表示法，那就是前缀和后缀表达式，也叫波兰和逆波兰，他们不需要括号，而且非常便于计算机处理，其实这些表达式的本质是一个语法树，前缀和后缀是最靠近树型结构的，这也是lisp家族语言的括号表达式的本质，他们本质就是对编程语言本质（抽象语法树）最自然的编码。

四则运算表达式的本质如图，是一个棵树

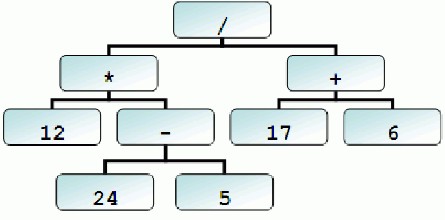
抽象语法树

我们可以用字母代替部分数字，比如 a + b * 2，给这个表达式一个环境,比如a =1,b=2 就可以得到最终运算结果,我们省略对语法树的构建，而是直接用语言支持的结构写出来，比如在ruby中，我们可以通过数组[:add, [:variable, :a], [:multiply, [:number, 2], [:variable, :b]]]来表达a + b * 2，现在让我们来看看各种语言怎么执行这些表达式，这些程序都包括了结构，运算，递归,函数语言还有模式匹配。

ruby的第一版本，通过符号匹配，然后运算

def evaluate(env, exp)
  keyword, a, b = exp
  case keyword
  when :number;   a
  when :variable; env[a]
  when :add;      evaluate(env, a) + evaluate(env, b)
  when :multiply; evaluate(env, a) * evaluate(env, b)
  end
end
 
ExpressionTree = [:add, [:variable, :a], [:multiply, [:number, 2], [:variable, :b]]]
Env = { a: 3, b: 4, c: 5 }
 
puts evaluate(Env, ExpressionTree)

上面第一个版本是通过case来寻找什么符号，然后再去找相应的运算，为何不去掉符号而直接把运算写在语法树中呢？那么有了ruby的第二版本，通过lambda表达式自执行

Number   = lambda { |env, num| num }
Variable = lambda { |env, var| env[var] }
Add      = lambda { |env, a, b| evaluate(env, a) + evaluate(env, b) }
Multiply = lambda { |env, a, b| evaluate(env, a) * evaluate(env, b) }
 
def evaluate(env, exp)
  op, *args = exp #并行赋值
  op.(env, *args) #执行
end
 
ExpressionTree = [Add, [Variable, :a], [Multiply, [Number, 2], [Variable, :b]]]
Env = { a: 3, b: 4, c: 5 }
 
puts evaluate(Env, ExpressionTree)

一个表达式的本质就是求值，它捕获环境，然后从环境中取值来计算，表达式应该是自封装的，比如a+b这个表达式应该封装运算和取值，至于是取a,取b还是取c由使用者决定，外部使用者通过指定取值key，比如a,b来创建一个封装体，封装体内部保存a和b，外部得到这个封装之后把它保存起来，这个封装体如果得到了环境就可以直接运行出结果，由于在编程语言中能够直接跑的就是函数，所以我们程序需要创建一个函数，同时这个函数有个环境保存取值key。由此，我们得到ruby实现的第三个版本，通过闭包，语法树不再是一个结构，而是一个闭包函数

在计算机科学中，我们把这种通过闭包变换来简化函数调用的方法叫做函数curry化。

def Number(num)      ->(env){ num } end
def Variable(var)    ->(env){ env[var] } end
def Add(f1, f2)      ->(env){ f1.(env)+f2.(env) } end
def Multiply(f1, f2) ->(env){ f1.(env)*f2.(env) } end

ExpressionTree = Add(Variable(:a), Multiply(Number(2), Variable(:b)))
Env = { a: 3, b: 4, c: 5 }

puts ExpressionTree.(Env)

用JavaScript翻译上面Ruby的实现，得到如下程序

var Number = function(n) { return function(env) { return n }};
var Add = function(e1, e2) { return function(env) { return e1(env) + e2(env) }};
var Variable = function(s) { return function(env) { return env[s] }};
var Multiply = function(e1, e2) { return function(env) { return e1(env) * e2(env) }};
var env = {a: 3, b: 4};
var result = Add(Variable("a"), Multiply(Number(2), Variable("b")))(env);

Lisp方言racket的实现，它可以直接解析表达式，但是要写成前缀表达式，这是lisp方言的S表达式写法

(define (evaluate env exp)
  (match exp
    [(? number? x)   x                                    ]
    [`(+ ,x ,y)      (+ (evaluate env x) (evaluate env y))]
    [`(* ,x ,y)      (* (evaluate env x) (evaluate env y))]
    [(? symbol? v)   (hash-ref env v)                     ]))

(define environment (hash 'a 3 'b 4 'c 5))
(define expression-tree '(+ a (* 2 b)))
(define result (evaluate environment expression-tree))

对于上面的写法，引入大侠wangyin的言论很好解释(分割线内)：

你必须从最简单的语言开始，逐步增加语言的复杂度，才能构造出正确的解释器。这篇文章就是告诉你如何写出一个最简单的语言 (lambda calculus) 的解释器，并且带有基本的的算术功能，可以作为一个高级计算器来使用。

一般的程序语言课程往往从语法分析(parsing)开始，折腾 lex 和 yacc 等麻烦却不中用的工具，解决一些根本不需要存在的问题。Parsing 的作用其实只是把字符串解码成程序的语法树（AST）结构。麻烦好久得到了 AST 之后，真正的困难才开始！而很多人在写完 parser 之后就已经倒下了。鉴于这个原因，这里我用所谓的“S-expression”来表示程序的语法树（AST）结构。S-expression （加上 Lisp 对它发自“本能”的处理能力）让我们可以直接跳过 parse 的步骤，进入关键的主题：语义(semantics)。

这里用的 Scheme 实现是 Racket。为了让程序简洁，我使用了 Racket 的模式匹配（pattern matching）。我对 Racket 没有特别的好感。但它安装比较方便，而且是免费的。如果你用其它的 Scheme 实现的话，恐怕要自己做一些调整。

Erlang VM 上的的语言Elixir，看看那个case

defmodule Ast do

  def eval(tree, env) do
      case tree do
        {:number, n}    -> n
        {:add, l, r}    -> eval(l, env) + eval(r, env)
        {:mul, l, r}    -> eval(l, env) * eval(r, env)
        {:variable, id} -> Dict.get(env, id)
      end
  end

  def start do
    env = HashDict.new [a: 1, b: 2, c: 3]
    tree = {:add, {:variable, :a}, {:mul, {:number, 2}, {:variable, :b}}}
    IO.puts  Ast.eval(tree, env)
  end

end

Ast.start

Scala的实现，也请注意那个case和match

abstract class Expression
 
case class Number(i: Int) extends Expression
case class Add(x: Expression, y: Expression) extends Expression
case class Multiply(x: Expression, y: Expression) extends Expression
case class Variable(id: Symbol) extends Expression
 
object Maths extends App {
  val environment = Map('a -> 1,
      'b -> 2,
      'c -> 3)
      
  def evaluate(env: Map[Symbol, Int], exp: Expression): Int = exp match {
    case Number(n: Int) => n    
    case Add(x, y) => evaluate(env, x) + evaluate(env, y)
    case Multiply(x, y) => evaluate(env, x) * evaluate(env, y)
    case Variable(id: Symbol) => env(id)
  }
      
  val expressionTree1 = Add(Variable('a), Multiply(Number(2), Variable('b)))
  
  println(evaluate(environment, expressionTree1))
}

参考资源

2013年/10月/18日 首页回退 各种语言的的四则运算AST实现

2013年/10月/18日
首页回退

各种语言的的四则运算AST实现